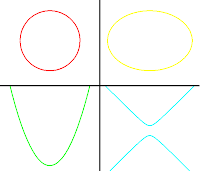
En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:
β < α : Hipérbola (azul)
β = α : Parábola (verde)
β > α : Elipse (amarillo)
β = 90º: Circunferencia (un caso particular de elipse) (rojo)
Si el plano pasa por el vértice del cono, se puede comprobar que:
Cuando β > α la intersección es un único punto (el vértice).
Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice. El ángulo formado por las rectas irá aumentando a medida β disminuye, hasta alcanzar el máximo (α) cuando el plano contenga al eje del cono (β = 0).
En coordenadas cartesianas, las cónicas se expresan en forma algebraica mediante ecuaciones cuadráticas de dos variables (x,y) de la forma:
ax2+2hxy+by2+2gx+2fy+c=0
No hay comentarios:
Publicar un comentario