Formula de la Pagina 23

d=Axo+Byo+C
--------------
A2+B2

Tema 5: distancia de un punto y la recta

Ser R una recta y Po un punto que no pertenece a R. La distancia de Po a r se define así: llamaremos r' a la recta que pasa por p0 y es perpendicular a r.

entonces r' corta r en un punto i, La distancia de Po a e es, por definición, la longitud del segmento po1.

Formula de la pagina 15

Y2-Y1 -(Y1-Y2) Y1-Y2
------ = ---------- = ---------
X2-X1 -(X1-X2) X1-X2

Formulas de punto medio

Ym = Xa + Xb -4 + 8
------------ = ----------- = 2
2 2


Ym= Ya + Yb 8 + 0
---------- = ------- = 4
2 2

ingresar imagen similar a la 1.11

Tema 4 pendiente de una recta

Concepto de pendiente de una recta.

Sea "r" una recta que pasa por los puntos P1 (X1 Y1) y P2 (X2, y2). Si X1 = X2, es decir, la recta es vertical o dicho de otro modo, su ángulo de inclinación es de 90°, la pendiente de R seria tan 90°, pero en este caso la tangente (Tan) no esta definida, no existe. por lo tanto. si los 2 puntos dados P1 y P2 tienen la misma abscisa, la recta r carece de pendiente, o sea, esta no existe.

Fórmula de distancia entre 2 puntos.

P1M= X2 - X1 Y MP2= Y2 - Y1

el teorema de pitagoras, aplicado al triangulo (delta) P1MP2 nos permite escribir que:


(P1P2)2 = (P1M)2 + (MP2)2 = (X2-X1)2 + (Y2-Y1)2

Tema 2: distancia entre 2 puntos, descripcion de una distancia entre 2 puntos

Sean P1 (X1,Y1) y P2 (X2, Y2) 2 puntos de coordenadas conocidas con las restricciones siguientes: X1 =X2 y Y1 = Y2. Esto significa que la recta P1P2 no es paralela a ninguno de los ejes coordenados.

Subir una imagen de un plano cartesiano y señalar los cuadrantes

Nombra los 2 ejes de un plano cartesiano

A una recta numérica se le llama también "eje", y en ocasiones, "recta orientada". El eje esta formado por 2 semi-ejes o 2 semi-rectas. el semi-eje positivo es el que tiene el origen en 0 y contiene al punto u, el otro semi-eje con origen en 0 y que contiene U' se llama, lógicamente, el semi-eje negativo.

¿Para que se utilizan?

Como creador de la geometría analítica, también comienza tomando un «punto de partida»: el sistema de referencia cartesiano, para poder representar la geometría plana tomando como referencia dos rectas perpendiculares entre sí, que se cortan en un punto denominado «origen de coordenadas», ideando las denominadas coordenadas cartesianas

¿Qué es un sistema de coordenadas cartesianas?

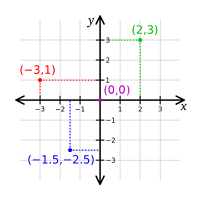
Las coordenadas cartesianas son un sistema de referencia respecto a un eje (recta), dos ejes (plano), o tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas (o rectangulares) x e y se denominan abscisa y ordenada respectivamente.

Tema 1: sistema de coordenadas cartesianas

¿Cual es el punto de partida de la geometría analítica?

el punto de partida de la geometría analítica son los llamados sistema de coordenadas cartesianas, mediante los cuales pueden ser resueltos, una gran variedad de problemas de geometría, empleando recursos de álgebra. Seguramente recordaras que en una recta numérica se pueden representar los números reales tanto los positivos como los negativos, los racionales y los irracionales. En dicha recta se escogen 2 puntos arbitrarios: O y U que van a ser las representaciones gráficas de los números con cero (0) y uno (1), respectivamente.

Las profesiones en las que se aplica el Cálculo Diferencial

Sin la geometría analítica es posible dominar el calculo diferencial e integral, las cuales constituyen a su vez, herramientas imprescindibles en la formación de ingenieros, físicos, matemáticos, químico, economistas, biólogos, agrónomos y otros profesionistas. Así pues, estos temas que se incluyen en el texto pueden ser de gran importancia para quien lo estudie.

Con la relación entre geometría analítica y álgebra surge el :

Con ello, se pudieron emplear los métodos utilizados por el álgebra en la solución de problemas planteados por la geometría y a la vez, apoyar con la geometría a los problemas planteados por el álgebra, dando origen a una nueva rama de la matemática: la geometría analítica. con su llegada de enriquecieron varias disciplinas, sentando así las bases para el surgimiento de una nueva rama de la matemática: el Calculo. Esto dio un gran impulso al desarrollo de la matemática.

Aportaciones de Rene Descartes

Aunque se conservan algunos apuntes de su juventud, su primera obra fue Reglas para la dirección del espíritu creada en 1628 y publicada en 1701.(póstuma). Luego escribió La luz o Tratado del mundo y El hombre, que retiró de la imprenta al enterarse de la condena de la Inquisición a Galileo en 1633, y que más tarde se publicaron a instancias de Leibniz. En 1637 publicó el Discurso del método para dirigir bien la razón y hallar la verdad en las ciencias, seguido de tres ensayos científicos: Dióptrica, La Geometría y Los meteoros. Con estas obras, escritas en francés, Descartes acaba por presentarse ante el mundo erudito, aunque inicialmente intentó conservar el anonimato.
En 1641 publicó las Meditaciones metafísicas, acompañadas de un conjunto de Objeciones y respuestas que amplió y volvió a publicar en 1642. Hacia 1642 puede fecharse también un diálogo, La búsqueda de la verdad mediante la razón natural (póstumo).
En 1647 aparecen los Principios de filosofía, que Descartes idealmente habría destinado a la enseñanza. En 1648 Descartes le concede una entrevista a Frans Burman, un joven estudiante de teología, quien le hace interesantes preguntas sobre sus textos filosóficos. Burman registra detalladamente las respuestas de Descartes, y éstas usualmente se consideran genuinas. En 1649 publica un último tratado, Las pasiones del alma, sin embargo aún pudo diseñar para Cristina de Suecia el reglamento de una sociedad científica, cuyo único artículo es que el turno de la palabra corresponda rotativamente a cada uno de los miembros, en un orden arbitrario y fijo.
De Descartes también se conserva una copiosa correspondencia, que en gran parte canalizaba a través de su amigo Mersenne, así como algunos esbozos y opúsculos que dejó inéditos. La edición de referencia de sus obras es la que prepararon Charles Adam y Paul Tannery a fines del siglo XIX e inicios del XX, y a la que los comentaristas usualmente se refieren como AT, por las iniciales de los apellidos de estos investigadores.

Concepto de algebra

El álgebra es la rama de las matemáticas que estudia las estructuras, las relaciones y las cantidades (en el caso del álgebra elemental). Junto a la geometría, el análisis matemático, la combinatoria y la teoría de números, el álgebra es una de las principales ramas de la matemática.

La palabra «álgebra» es de origen árabe, deriva del tratado escrito por el matemático persa Muhammad ibn Musa al-Jwarizmi, titulado Al-Kitab al-Jabr wa-l-Muqabala (en árabe كتاب الجبر والمقابلة) (que significa "Compendio de cálculo por el método de completado y balanceado"), el cual proporcionaba operaciones simbólicas para la solución sistemática de ecuaciones lineales y cuadráticas. Etimológicamente, la palabra «álgebra» (también nombrado por los árabes Amucabala) جبر (yebr) (al-dejaber), proviene por lo tanto del árabe y significa "reducción", operación de cirugía por la cual se reducen los huesos luxados o fraccionados (algebrista era el médico reparador de huesos).

Concepto de geometría analítica

La geometría y el algebra son ramas de las matematicas que se fueron desarrollando de forma independiente hasta el siglo XVll, cuando el matematico y filosofo rene descartes escribio una obra* en la que incluia un tema sobre geometria, en donde establece una relacion entre esta rama de la matematica con el algebra, al elaborar el metodo de las coordenadas como una forna de localizar cualquier punto en el plano.

Derivadas de orden superior

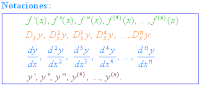
Sea f una función diferenciable, entonces se dice que f ' es la primera derivada de f; puede suceder que esta nueva función sea a su vez derivable, en este caso a la derivada de la primera derivada se le denomina segunda derivada de la función primitiva f. Del mismo modo, la derivada de la segunda derivada se llama tercera derivada de f, y así sucesivamente hasta la enésima derivada.

Puntos Máximos y Mínimos

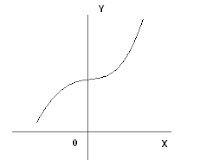
Con cierta frecuencia nos encontramos con la necesidad de buscar la mejor forma de hacer algo. En muchas ocasiones a través de los poderosos mecanismos de cálculo diferencial es posible encontrar respuesta a estos problemas, que de otro modo parecería imposible su solución.
Entre los valores q puede tener una función (Y) puede haber uno que sea el mas grande y otro que sea el mas pequeño. A estos valores se les llama respectivamente punto máximo y punto mínimo absolutos.
Si una función continua es ascendente en un intervalo y a partir de un punto cualquiera empieza a decrecer, a ese punto se le conoce como punto critico máximo relativo, aunque comúnmente se le llama solo máximo.
Por el contrario, si una funcion continua es decreciente en cierto intervalo hasta un punto en el cual empieza a ascender, a este punto lo llamamos puntro critico minimo relativo, o simplemente minimo.
Una funcion puede tener uno, ninguno o varios puntos criticos.
Curva sin máximos ni mínimos función sin máximos ni mínimos


METODOS PARA CALCULAR MAXIMOS Y MINIMOS DE UNA FUNCION
Para conocer las coordenadas de los puntos críticos máximos y mínimos relativos en una función, analizaremos dos mecanismos:
CRITERIO DE LA PRIMERA DERIVADA, UTILIZADO PARA UNA FUNCION CONTINUA Y SU PRIMERA DERIVADA TAMBIEN CONTINUA.
obtener la primera derivada.
igualar la primera derivada a cero y resolver la ecuación.
El valor o valores obtenidos para la variable, son donde pudiera haber máximos o mínimos en la función.
se asignan valores próximos (menores y mayores respectivamente) a la variable independiente y se sustituyen en la derivada. Se observan los resultados; cuando estos pasan de positivos a negativos, se trata de un punto máximo; si pasa de negativo a positivo el punto crítico es mínimo.
Cuando existen dos o más resultados para la variable independiente, debe tener la precaución de utilizar valores cercanos a cada uno y a la vez distante de los demás, a fin de evitar errores al interpretar los resultados.
sustituir en la función original (Y) el o los valores de la variable independiente (X) para los cuales hubo cambio de signo. Cada una de las parejas de datos así obtenidas, corresponde a las coordenadas de un punto crítico.
CRITERIO DE LA SEGUNDA DERIVADA
Este método es más utilizado que el anterior, aunque no siempre es más sencillo. Se basa en que en un máximo relativo, la concavidad de una curva es hacia abajo y en consecuencia, su derivada será negativa; mientras que en un punto mínimo relativo, la concavidad es hacia arriba y la segunda derivada es positiva.
Este procedimiento consiste en:
calcular la primera y segunda derivadas
igualar la primera derivada a cero y resolver la ecuación.
sustituir las raíces (el valor o valores de X) de la primera derivada en la segunda derivada.
Si el resultado es positivo, hay mínimo. Si la segunda derivada resulta negativa, hay un máximo.
Si el resultado fuera cero, no se puede afirmar si hay o no un máximo o mínimo.
sustituir los valores de las raíces de la primera derivada en la función original, para conocer las coordenadas de los puntos máximo y mínimo

Funciones Cónicas

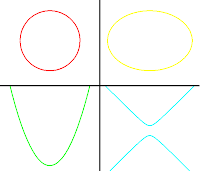
En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:
β < α : Hipérbola (azul)
β = α : Parábola (verde)
β > α : Elipse (amarillo)
β = 90º: Circunferencia (un caso particular de elipse) (rojo)
Si el plano pasa por el vértice del cono, se puede comprobar que:
Cuando β > α la intersección es un único punto (el vértice).
Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).
Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice. El ángulo formado por las rectas irá aumentando a medida β disminuye, hasta alcanzar el máximo (α) cuando el plano contenga al eje del cono (β = 0).


En coordenadas cartesianas, las cónicas se expresan en forma algebraica mediante ecuaciones cuadráticas de dos variables (x,y) de la forma:

ax2+2hxy+by2+2gx+2fy+c=0

La Derivada

En geometría, la derivada de una función en un punto representa el valor de la pendiente de la recta tangente en dicho punto. La pendiente está dada por la tangente del ángulo que forma la recta tangente a la curva (función) con el eje de las abscisas, en ese punto.
La derivada de una función mide el coeficiente de variación de dicha función. Es decir, provee una formulación matemática de la noción del coeficiente de cambio. El coeficiente de cambio indica lo rápido que crece (o decrece) una función en un punto (razón de cambio promedio) respecto del eje de un plano cartesiano de dos dimensiones. Por ejemplo, si tomamos la velocidad de un móvil, su coeficiente es la aceleración, la cual mide cuánto cambia la velocidad en un tiempo dado.

dada la ecuación Y= x

-----------

x2 + 1

En esta tabla se obtienen valores para puntos (x,y) que pueden ser graficados en un plano cartesiano con ejes X e Y . En lenguaje matemático la palabra "función" se expresa sustituyendo la variable Y por la expresión F (x) e indicando así que es F una función, en este caso evaluada con la letra X . En lenguaje coloquial F (x) se lee "efe de equis". Así pues en la ecuación anterior el valor de la variable Y viene dado por F (x) donde Y= x

-------

x2 + 1

la primer tabla deberia estar aqui abajo pero ... no se como ponerla

La Circunferencia

Una circunferencia es el lugar geométrico de los puntos del plano equidistantes de otro fijo, llamado centro; esta distancia se denomina radio. Sólo posee longitud. Se distingue del círculo en que este es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.
Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio.

Elementos de la circunferencia

Existen varios puntos, rectas y segmentos, singulares en la circunferencia:

Centro, el punto interior equidistante de todos los puntos de la circunferencia;
Radio, el segmento que une el centro con un punto de la circunferencia;
diámetro, el mayor segmento que une dos puntos de la circunferencia, y lógicamente, pasa por el centro;
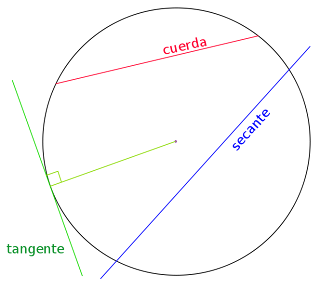
Cuerda, el segmento que une dos puntos de la circunferencia; las cuerdas de longitud máxima son los diámetros;
Recta secante, la que corta a la circunferencia en dos puntos;
Recta tangente, la que toca a la circunferencia en un sólo punto;
punto de tangencia, el de contacto de la tangente con la circunferencia;
Arco, segmento curvilíneo de puntos pertenecientes a la circunferencia;
Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.

La Parábola

Una parábola es el lugar geométrico de los puntos equidistantes de una recta dada, llamada directriz, y un punto fijo que se denomina foco.

Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.

La ecuación de una parábola cuyo eje es vertical y su vértice es (u,v) tiene la forma (y-v)=a(x-u)2,

La ecuación de una parábola cuyo eje es vertical es de la forma .

La ecuación de una parábola cuyo eje es horizontal es de la forma .